11 Lab: Data Processing and Summarization

Here we will be exploring different functions in data processing and summarization.

import warnings
warnings.filterwarnings('ignore')

# Importing libraries
import numpy as np
import pandas as pd
# statsmodels below is a Python module for statistical data exploration, testing, and modelling  
import statsmodels.api as sm
from scipy.spatial.distance import cdist # this is a function that computes the Mahalanobis distance
from scipy.stats import skew, kurtosis # the skew and kurtosis of a distribution - (re)watch the video lectures if you need a reminder of skew & curtosis
from statsmodels.robust.scale import mad # this computes the median absolute deviation of a distribution
import matplotlib.pyplot as plt
import seaborn as sns
#%matplotlib inline #display matplotlib plots inline with the text. +info: https://stackoverflow.com/a/43028034/1913457

11.1 Outliers

In this section we will be applying several methods to identify outliers. We will be using a custom dataset called accord_sedan.csv that contains data on cars and their properties. The dataset is provided as a csv file within the data/raw folders.

11.1.1 Assess data

As usual, we will want to start loading the data and inspecting it (remember spreadsheet software like Excel is also your friend to inspect data):

# Loading Data
df = pd.read_csv('data/raw/accord_sedan.csv')

# Inspecting the few first rows of the dataframe
df.head()

	price	mileage	year	trim	engine	transmission
0	14995	67697	2006	ex	4 Cyl	Manual
1	11988	73738	2006	ex	4 Cyl	Manual
2	11999	80313	2006	lx	4 Cyl	Automatic
3	12995	86096	2006	lx	4 Cyl	Automatic
4	11333	79607	2006	lx	4 Cyl	Automatic

And we can get some summary statistics, too:

df.describe()

	price	mileage	year
count	417.000000	417.000000	417.0
mean	12084.242206	89725.779376	2006.0
std	2061.430034	25957.872271	0.0
min	6900.000000	19160.000000	2006.0
25%	10779.000000	71844.000000	2006.0
50%	11995.000000	89900.000000	2006.0
75%	13000.000000	106705.000000	2006.0
max	18995.000000	149269.000000	2006.0

Do this yourself:

We only get the summaries for the numeric values here. How about the others, such as trim, engine or transmission? You can also use df.columns.tolist() to see a list of column names in your dataframe.

Some questions for reflection (discuss with your peers):

What descriptive statistics would you use to summarise the distribution of these values?
Do you think the mean of the ‘year’ values make sense? What could be a better statistical measure instead?

## one thing to try is the describe function with an "all" parameter:
df.describe(include='all')

	price	mileage	year	trim	engine	transmission
count	417.000000	417.000000	417.0	417	417	417
unique	NaN	NaN	NaN	3	2	2
top	NaN	NaN	NaN	ex	4 Cyl	Automatic
freq	NaN	NaN	NaN	288	238	382
mean	12084.242206	89725.779376	2006.0	NaN	NaN	NaN
std	2061.430034	25957.872271	0.0	NaN	NaN	NaN
min	6900.000000	19160.000000	2006.0	NaN	NaN	NaN
25%	10779.000000	71844.000000	2006.0	NaN	NaN	NaN
50%	11995.000000	89900.000000	2006.0	NaN	NaN	NaN
75%	13000.000000	106705.000000	2006.0	NaN	NaN	NaN
max	18995.000000	149269.000000	2006.0	NaN	NaN	NaN

# But this doesn't address our question. Think about visuals that can help you here? Maybe a histrogram would help?
sns.histplot(data=df, x="price")

# You can, of course, explore the distributions of other features in your dataset, so feel free to insert cells below to create more visualisations

# Now focusing on descriptive statistics for the categorical columns, you can pass 'category' 
# as an argument to the describe function alongside indicating you wish to focus on the object columns (not numeric ones).
# Read more here https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.describe.html
df.describe(include=["object", "category"])

	trim	engine	transmission
count	417	417	417
unique	3	2	2
top	ex	4 Cyl	Automatic
freq	288	238	382

Once you have an idea of the descriptive statistics, you might want to focus on the outliers. It might be difficult to spot outliers just with the descriptive statistics. This is where we can use data visualisations to identify outliers visually and also make use of a few proxy metrics to help us assess data points.

11.1.2 Identify outliers visually

In this case we will explore variables individually (1D) by creating a boxplot¹. We will visualise the columns price and mileage using matplotlib’s subplots, which combines multiple plots into a single figure:

¹ Boxplots may be difficult to interpret if we are not used to them. It is used to visualise distributions, where the box represents the Interquartile range (IQR), whereas the whiskers can be defined in multiple ways (e.g. the first and third quartiles, 1.5 IQR…). 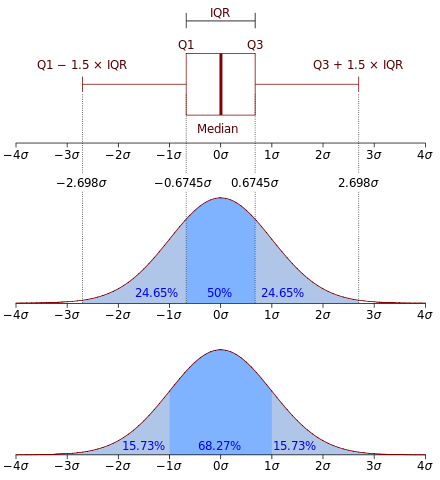See this week’s videos on Moodle if you’d like a refresher on IQR or other topics covered in the Python notebooks.

From Wikipedia: “In descriptive statistics, a box plot or boxplot is a method for graphically demonstrating the locality, spread and skewness groups of numerical data through their quartiles.”

A visualisation depicting how a Box Plot works. Source: Wikipedia

# 1D visualisation
plt.figure(figsize=(9, 5)) # setting the figure's size: format width, height (in inches)
plt.subplot(1,2,1) # subplot(nrows, ncols, index, **kwargs)
plt.boxplot(df.price)
plt.title("Boxplot of the Price attribute")
plt.subplot(1,2,2)
plt.boxplot(df.mileage)
plt.title("Boxplot of the Mileage attribute");
# a semicolon in Python denotes separation, rather than termination. 
# It allows you to write multiple statements on the same line.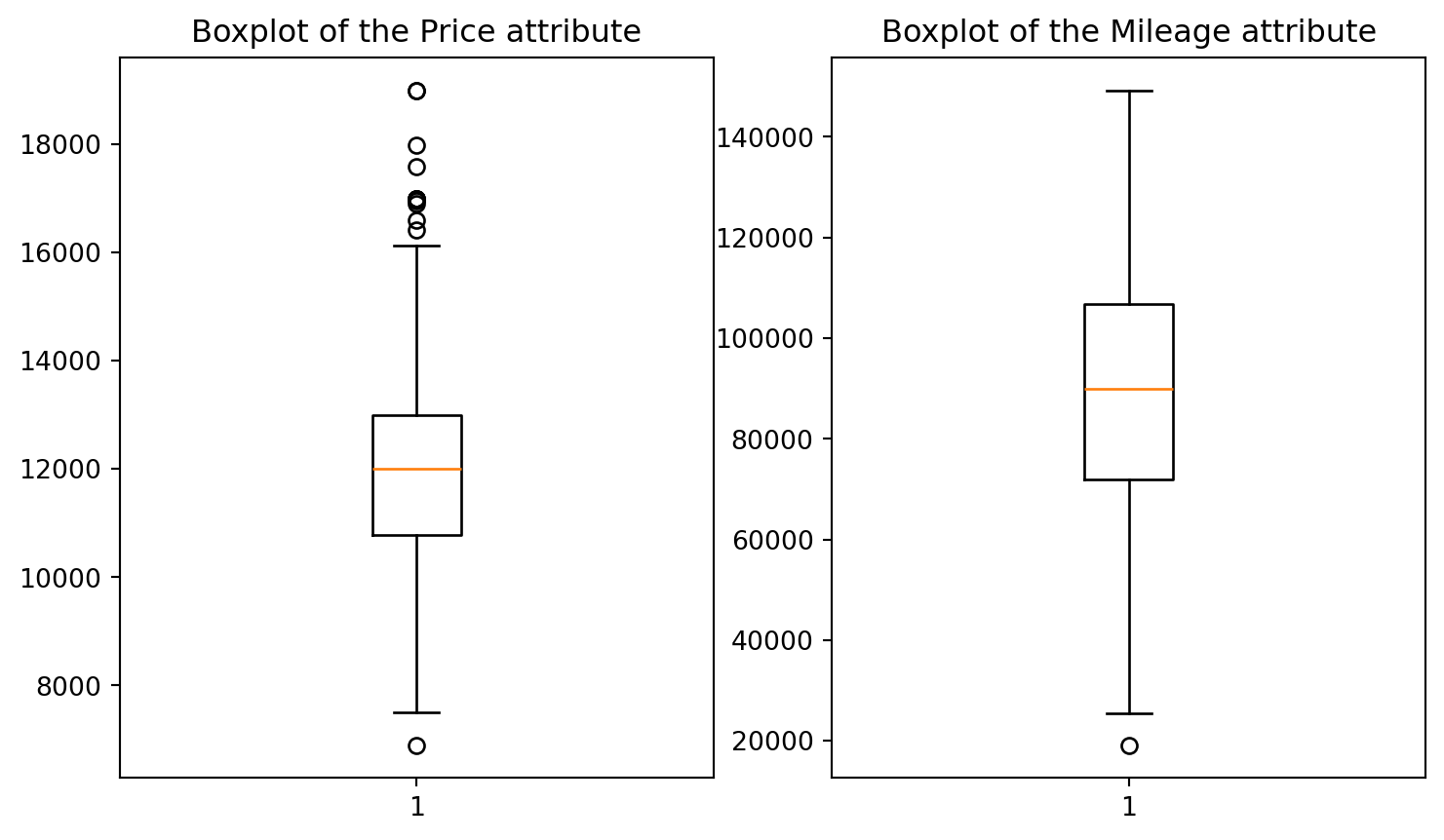

But we may want to identify the 2D outliers using a scatterplot

# 2D visualisation
plt.scatter(df.price, df.mileage, alpha = 0.5)
plt.xlabel('Price')
plt.ylabel('Mileage')
plt.title('Mileage vs. Price\n');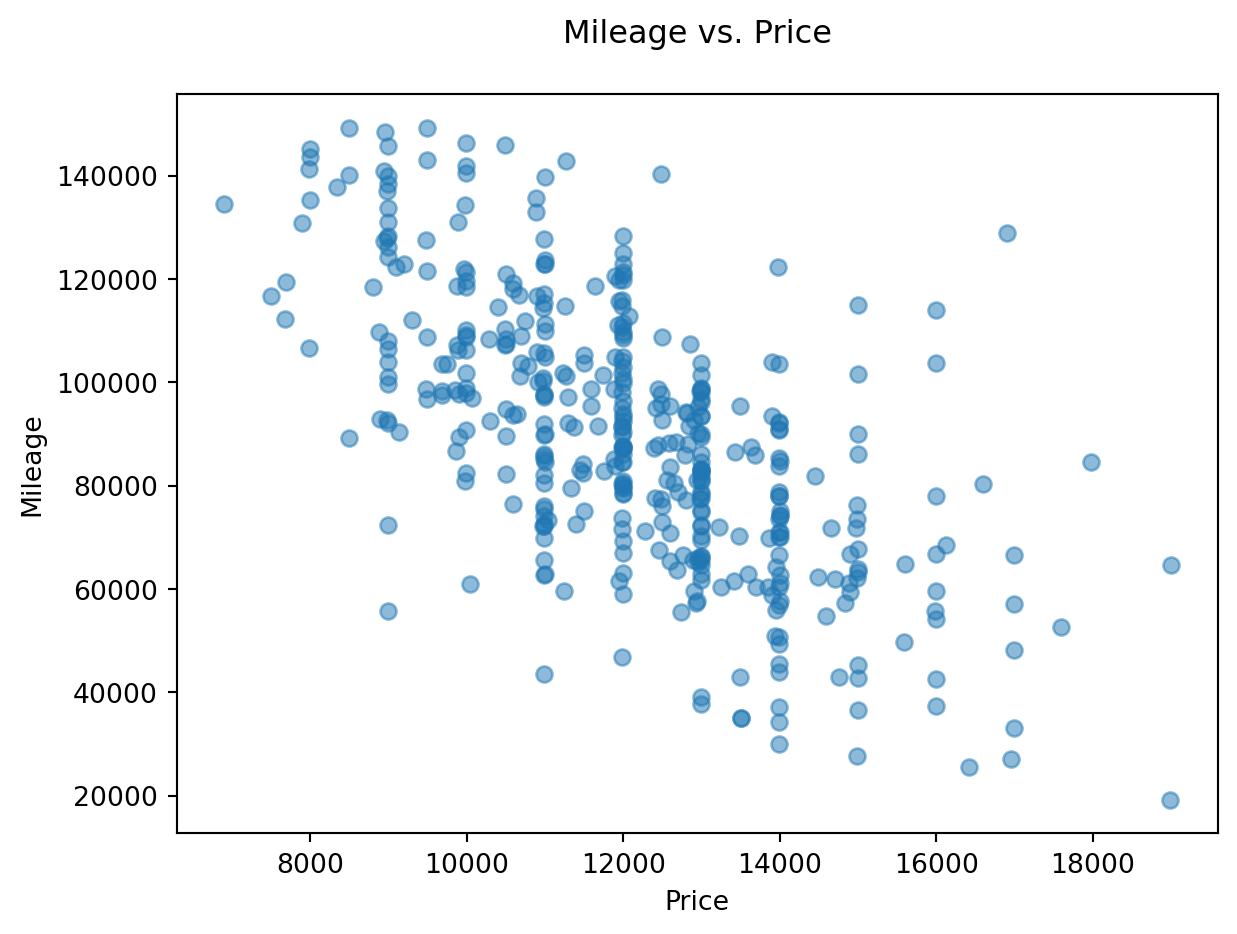

Note

Visually, outliers appear to be outside the ‘normal’ range of the rest of the points. A few outliers are quite obvious to spot, but the choice of the threshold (the limit after which you decide to label a point as an outlier) visually remains a very subjective matter.

11.1.3 Computing outliers’ threshold: standard deviation

Add two new columns to the dataframe called isOutlierPrice and isOutlierMileage. We will define our threshold as 2 times standard deviations away from the mean for price and mileage, respectively.

You may recall from this week’s videos that, if your data is normally distributed (revisit the histogram above as a reminder), approximately 95% of data points will fall within 2 standard deviations of the mean.

# Computing the isOutlierPrice column
upper_threshold_price = df.price.mean() + 2*df.price.std() 
lower_threshold_price = df.price.mean() - 2*df.price.std()
df['isOutlierPrice'] = ((df.price > upper_threshold_price) | (df.price < lower_threshold_price))

# Computing the isOutlierMileage column
upper_threshold_mileage = df.mileage.mean() + 2*df.mileage.std()
lower_threshold_mileage = df.mileage.mean() - 2*df.mileage.std()
df['isOutlierMileage'] = ((df.mileage > upper_threshold_mileage) | (df.mileage < lower_threshold_mileage))

# Inspect the new DataFrame with the added columns
df.head()

	price	mileage	year	trim	engine	transmission	isOutlierPrice	isOutlierMileage
0	14995	67697	2006	ex	4 Cyl	Manual	False	False
1	11988	73738	2006	ex	4 Cyl	Manual	False	False
2	11999	80313	2006	lx	4 Cyl	Automatic	False	False
3	12995	86096	2006	lx	4 Cyl	Automatic	False	False
4	11333	79607	2006	lx	4 Cyl	Automatic	False	False

Alternative method

We may want to do the above using a more succint approach:

# The np.where() function becomes handy
# The condition checks whether the absolute difference between a row’s price and the mean price of the entire column is less than 2 SDs of the price column. 
# If the condition is met, the computed value is False (not an Outlier), or True (an Outlier) if not.
df['isOutlierPrice'] = np.where(abs(df.price - df.price.mean()) < 2*df.price.std(), False, True)
df['isOutlierMileage'] = np.where(abs(df.mileage - df.mileage.mean()) < 2*df.mileage.std(), False, True)

# inspect the new DataFrame with the added columns
df.head()

	price	mileage	year	trim	engine	transmission	isOutlierPrice	isOutlierMileage
0	14995	67697	2006	ex	4 Cyl	Manual	False	False
1	11988	73738	2006	ex	4 Cyl	Manual	False	False
2	11999	80313	2006	lx	4 Cyl	Automatic	False	False
3	12995	86096	2006	lx	4 Cyl	Automatic	False	False
4	11333	79607	2006	lx	4 Cyl	Automatic	False	False

As we’d expect, both methods produce the same output.

Now that we have these two new columns, we could visualize these values with a different color in the plot. Observe whether they are the same as you would mark them:

# visualising outliers in a different color
col = ['tomato' if i+j else 'seagreen' for i,j in zip(df.isOutlierPrice, df.isOutlierMileage)]
plt.scatter(df.price, df.mileage, color = col)
plt.xlabel('Price')
plt.ylabel('Mileage')
plt.title('Mileage vs. Price : Outliers 2+ std\'s away from the mean\n');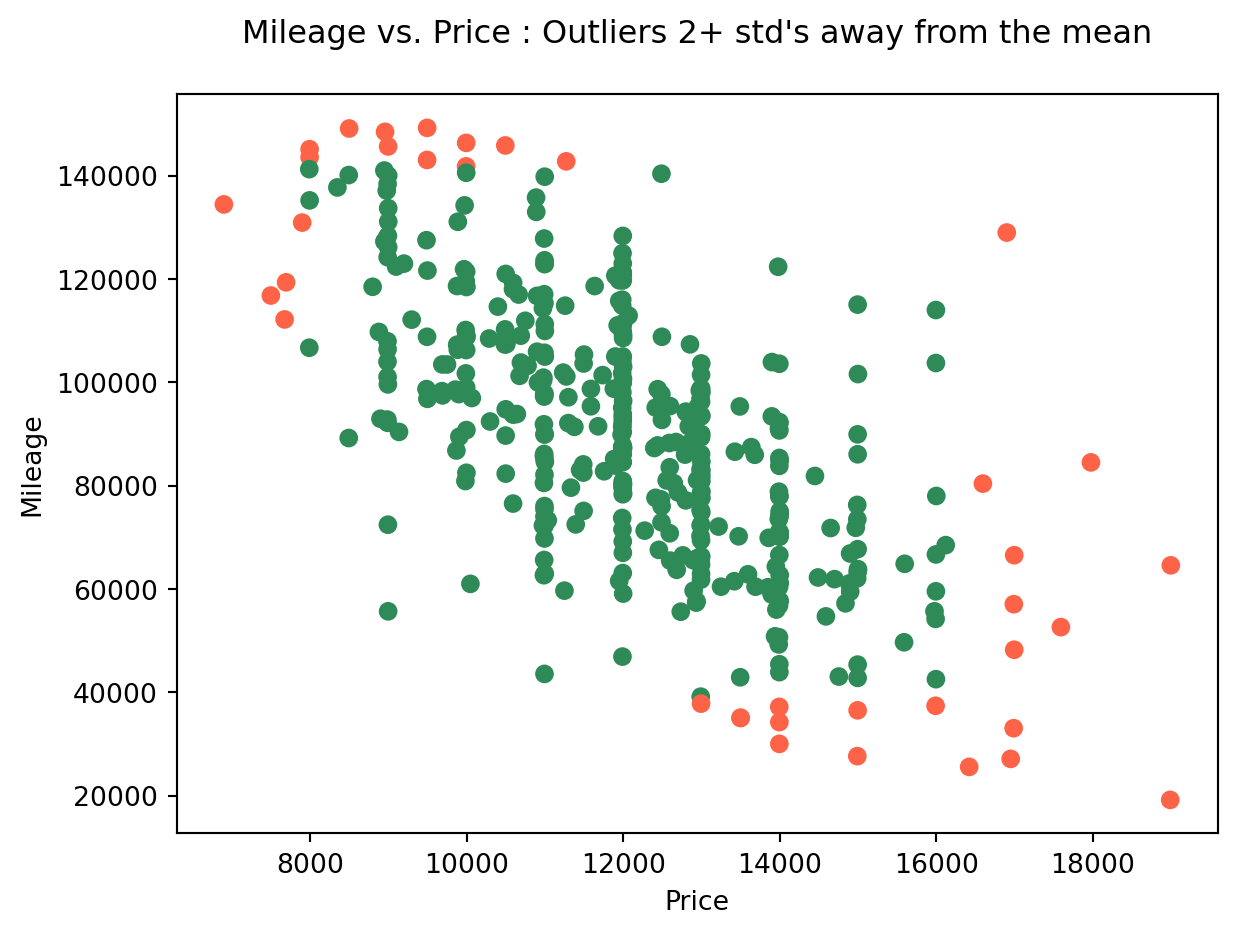

Visually filtering out outliers can be an effective tactic if we’re just trying to conduct a quick and dirty experimentation. However, when we need to perform a solid and founded analysis, it’s better to have a robust justification for our choices.

In this case, we can use the deviation from the mean to define a threshold that separates ‘normal’ values from ‘outliers’. Here, we opted for a two standard deviation threshold.

The mathematical intuition behind this, is that under the normality assumption (if we assume our variable is normally distributed, which it often is – see below), then the probability of it having a value two SDs OR MORE away from the mean, is around 5%, which is very unlikely to happen. This is why we label these data points as outliers with respect to the (assumed) probability distribution of the variable. But this remains a way to identify 1D outliers only (identifying outliers within each column separately)

# histograms of Price and Mileage (checking the normality assumption)
plt.subplot(1,2,1)
plt.hist(df.price, bins = 12)
plt.title('Price')
plt.subplot(1,2,2)
plt.hist(df.mileage, bins = 15)
plt.title('Mileage');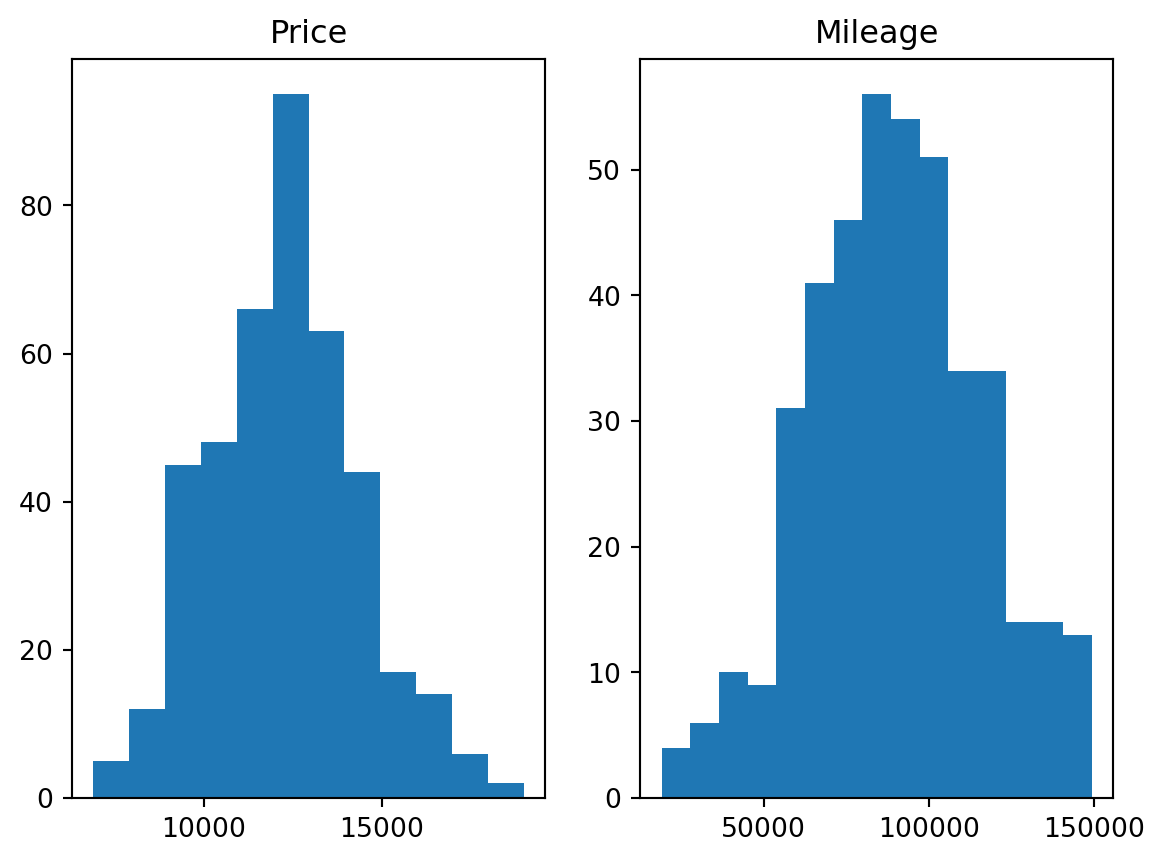

11.1.4 Computing outliers’ threshold: Mahalanobis distance

Using the 2D Mahalanobis distance to find outliers

# mean vector (computing the mean returns a Series, which we need to convert back to a DataFrame because cdist requires it)
mean_v = df.iloc[:, 0:2].mean().to_frame().T # DataFrame.T returns the Transpose of the DataFrame
#mean_v = np.asarray([df.price.mean(), df.mileage.mean()]).reshape(1,2) # This is a better way of writing the line before (for our use case : cdist function)

# computing the Mahalanobis distance of each row to the mean vector using cdist from the scipy library
d = cdist(df.iloc[:, 0:2], mean_v, metric='mahalanobis')
#d = cdist(df[['price', 'mileage']].values, mean_v, metric='mahalanobis') # Another way of writing the line before

# visualizing the scatter plot while coloring each point (i.e row) with a color from a chosen gradient colormap corresponding to the mahalanobis score
plt.figure(figsize=(12, 5))
plt.scatter(df.price, df.mileage, c = d.flatten(), cmap = 'plasma') 
# in order to know why we use flatten() on d above, try printing d with and without flatten
# cue: it has something to do with Data Structures in Python, see https://www.codecademy.com/article/python-data-structures for an accessible overview
plt.colorbar() # to show the colorbar
plt.xlabel('Price')
plt.ylabel('Mileage')
plt.title('Mileage vs. Price colored by a 2D Mahalanobis score\n');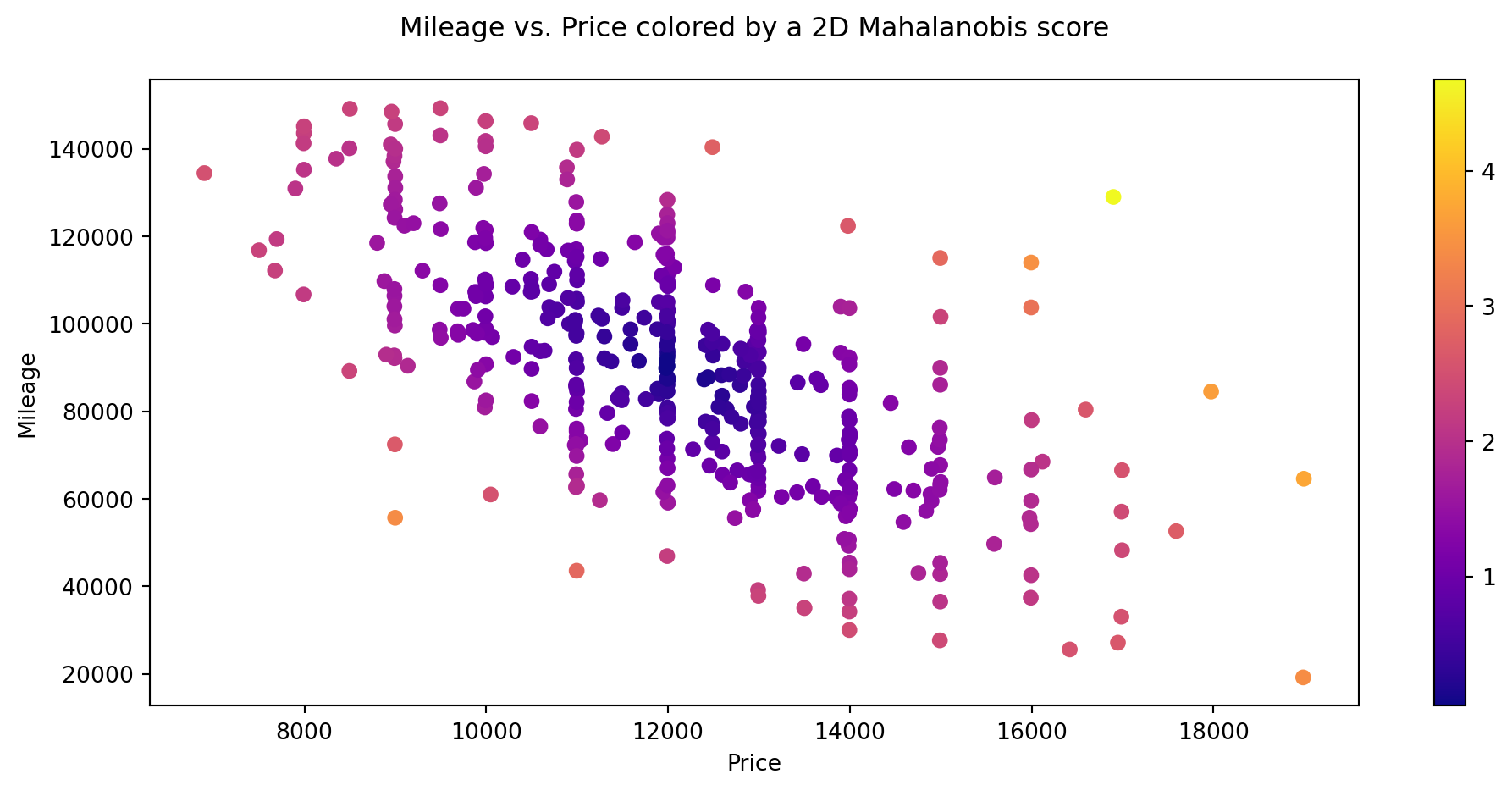

11.2 Q-Q Plots

11.2.1 Data

In this case, we will be using data reported by countries to WHO and estimates of tuberculosis burden generated by WHO for the Global Tuberculosis Report, as part of WHO’s Global Tuberculosis Programme. You can refer to this section at WHO’s website to know more about the data and their variables.

For your convenience, we have stored a copy in a csv file, but you could try to replicate the code with more up-to-date data from the original website. As usual, it is a best practice to explore the data before proceeding any further:

# Getting the Data
df_tuber = pd.read_csv('data/raw/TB_burden_countries_2014-09-29.csv')

df_tuber.head()

	country	iso2	iso3	iso_numeric	g_whoregion	year	e_pop_num	e_prev_100k	e_prev_100k_lo	e_prev_100k_hi	...	e_inc_tbhiv_100k	e_inc_tbhiv_100k_lo	e_inc_tbhiv_100k_hi	e_inc_tbhiv_num	e_inc_tbhiv_num_lo	e_inc_tbhiv_num_hi	source_tbhiv	c_cdr	c_cdr_lo	c_cdr_hi
0	Afghanistan	AF	AFG	4	EMR	1990	11731193	327.0	112.0	655.0	...	0.35	0.22	0.52	41.0	25.0	60.0	Model	20.0	13.0	32.0
1	Afghanistan	AF	AFG	4	EMR	1991	12612043	359.0	172.0	613.0	...	0.36	0.19	0.58	45.0	24.0	73.0	Model	97.0	77.0	120.0
2	Afghanistan	AF	AFG	4	EMR	1992	13811876	387.0	169.0	693.0	...	0.37	0.19	0.62	51.0	26.0	86.0	Model	NaN	NaN	NaN
3	Afghanistan	AF	AFG	4	EMR	1993	15175325	412.0	186.0	724.0	...	0.38	0.20	0.63	58.0	30.0	95.0	Model	NaN	NaN	NaN
4	Afghanistan	AF	AFG	4	EMR	1994	16485018	431.0	199.0	751.0	...	0.40	0.21	0.64	65.0	35.0	100.0	Model	NaN	NaN	NaN

5 rows × 39 columns

df_tuber.info()

<class 'pandas.DataFrame'>
RangeIndex: 4903 entries, 0 to 4902
Data columns (total 39 columns):
 #   Column                    Non-Null Count  Dtype  
---  ------                    --------------  -----  
 0   country                   4903 non-null   str    
 1   iso2                      4880 non-null   str    
 2   iso3                      4903 non-null   str    
 3   iso_numeric               4903 non-null   int64  
 4   g_whoregion               4903 non-null   str    
 5   year                      4903 non-null   int64  
 6   e_pop_num                 4903 non-null   int64  
 7   e_prev_100k               4892 non-null   float64
 8   e_prev_100k_lo            4892 non-null   float64
 9   e_prev_100k_hi            4892 non-null   float64
 10  e_prev_num                4892 non-null   float64
 11  e_prev_num_lo             4892 non-null   float64
 12  e_prev_num_hi             4892 non-null   float64
 13  e_mort_exc_tbhiv_100k     4902 non-null   float64
 14  e_mort_exc_tbhiv_100k_lo  4902 non-null   float64
 15  e_mort_exc_tbhiv_100k_hi  4902 non-null   float64
 16  e_mort_exc_tbhiv_num      4902 non-null   float64
 17  e_mort_exc_tbhiv_num_lo   4902 non-null   float64
 18  e_mort_exc_tbhiv_num_hi   4902 non-null   float64
 19  source_mort               4902 non-null   str    
 20  e_inc_100k                4902 non-null   float64
 21  e_inc_100k_lo             4902 non-null   float64
 22  e_inc_100k_hi             4902 non-null   float64
 23  e_inc_num                 4902 non-null   float64
 24  e_inc_num_lo              4902 non-null   float64
 25  e_inc_num_hi              4902 non-null   float64
 26  e_tbhiv_prct              3653 non-null   float64
 27  e_tbhiv_prct_lo           3457 non-null   float64
 28  e_tbhiv_prct_hi           3457 non-null   float64
 29  e_inc_tbhiv_100k          3597 non-null   float64
 30  e_inc_tbhiv_100k_lo       3597 non-null   float64
 31  e_inc_tbhiv_100k_hi       3597 non-null   float64
 32  e_inc_tbhiv_num           3597 non-null   float64
 33  e_inc_tbhiv_num_lo        3597 non-null   float64
 34  e_inc_tbhiv_num_hi        3597 non-null   float64
 35  source_tbhiv              4902 non-null   str    
 36  c_cdr                     4476 non-null   float64
 37  c_cdr_lo                  4476 non-null   float64
 38  c_cdr_hi                  4476 non-null   float64
dtypes: float64(30), int64(3), str(6)
memory usage: 1.5 MB

As you can see we have a pretty large dataset numerical and categorical variables, some of which have many missing values. In this case we will be filling missing values with the mean²

² Refer to Section 8.2 for a detailed explanation and alternative methods to deal with missing values.

# Filling missing numeric values ONLY (categorical values will be untouched)
df_tuber = df_tuber.fillna(value=df_tuber.mean(numeric_only = True))

# Count missing values
df_tuber.isna().sum()

country                      0
iso2                        23
iso3                         0
iso_numeric                  0
g_whoregion                  0
year                         0
e_pop_num                    0
e_prev_100k                  0
e_prev_100k_lo               0
e_prev_100k_hi               0
e_prev_num                   0
e_prev_num_lo                0
e_prev_num_hi                0
e_mort_exc_tbhiv_100k        0
e_mort_exc_tbhiv_100k_lo     0
e_mort_exc_tbhiv_100k_hi     0
e_mort_exc_tbhiv_num         0
e_mort_exc_tbhiv_num_lo      0
e_mort_exc_tbhiv_num_hi      0
source_mort                  1
e_inc_100k                   0
e_inc_100k_lo                0
e_inc_100k_hi                0
e_inc_num                    0
e_inc_num_lo                 0
e_inc_num_hi                 0
e_tbhiv_prct                 0
e_tbhiv_prct_lo              0
e_tbhiv_prct_hi              0
e_inc_tbhiv_100k             0
e_inc_tbhiv_100k_lo          0
e_inc_tbhiv_100k_hi          0
e_inc_tbhiv_num              0
e_inc_tbhiv_num_lo           0
e_inc_tbhiv_num_hi           0
source_tbhiv                 1
c_cdr                        0
c_cdr_lo                     0
c_cdr_hi                     0
dtype: int64

Pick one of the columns from the Tuberculosis data and copy it into a numpy array as before

# Picking a column (I created a variable for this so I (and you (: ) can modify the column easily here and the change will be carried out everywhere I use the variable colname)
colname = 'e_prev_100k'

# Creating a numpy array from our column
col = np.array(df_tuber[colname])

# Printing the type of our newly created column
print(type(col))

<class 'numpy.ndarray'>

Compare this selected column to a Normal distribution. Then Sample from a Normal distribution and show a second Q-Q plot

# Plotting the Q-Q Plot for our column
sm.qqplot(col, line='r')
plt.title('Q-Q Plot of the "{}" column of our dataset'.format(colname));

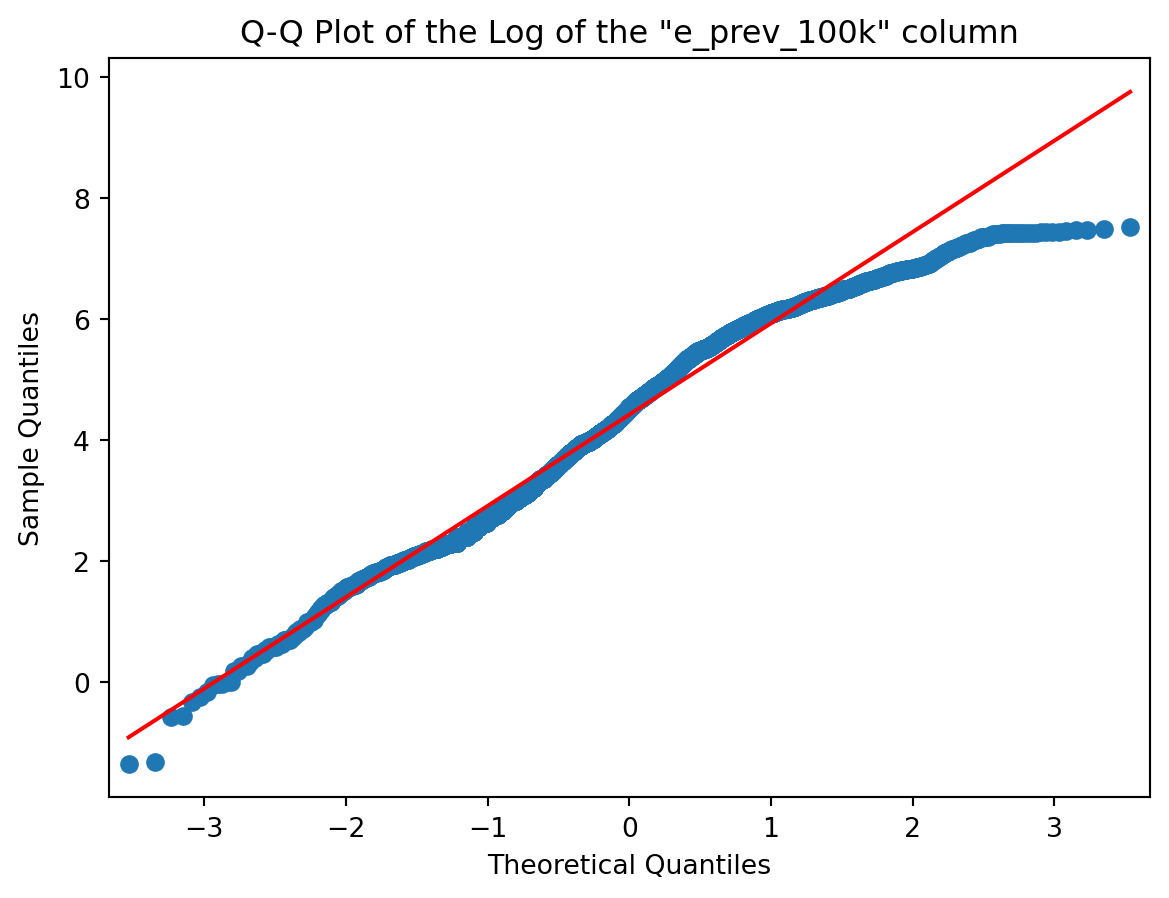
# Plotting the Q-Q Plot for the log of our column
sm.qqplot(np.log(col), line='r')
plt.title('Q-Q Plot of the Log of the "{}" column'.format(colname));

# Sampling from a Gaussian and a uniform distribution
sample_norm = np.random.randn(1000)
sample_unif = np.random.rand(1000)

# Plotting the second Q-Q Plot for our sample (that was generated using a normal distribution)
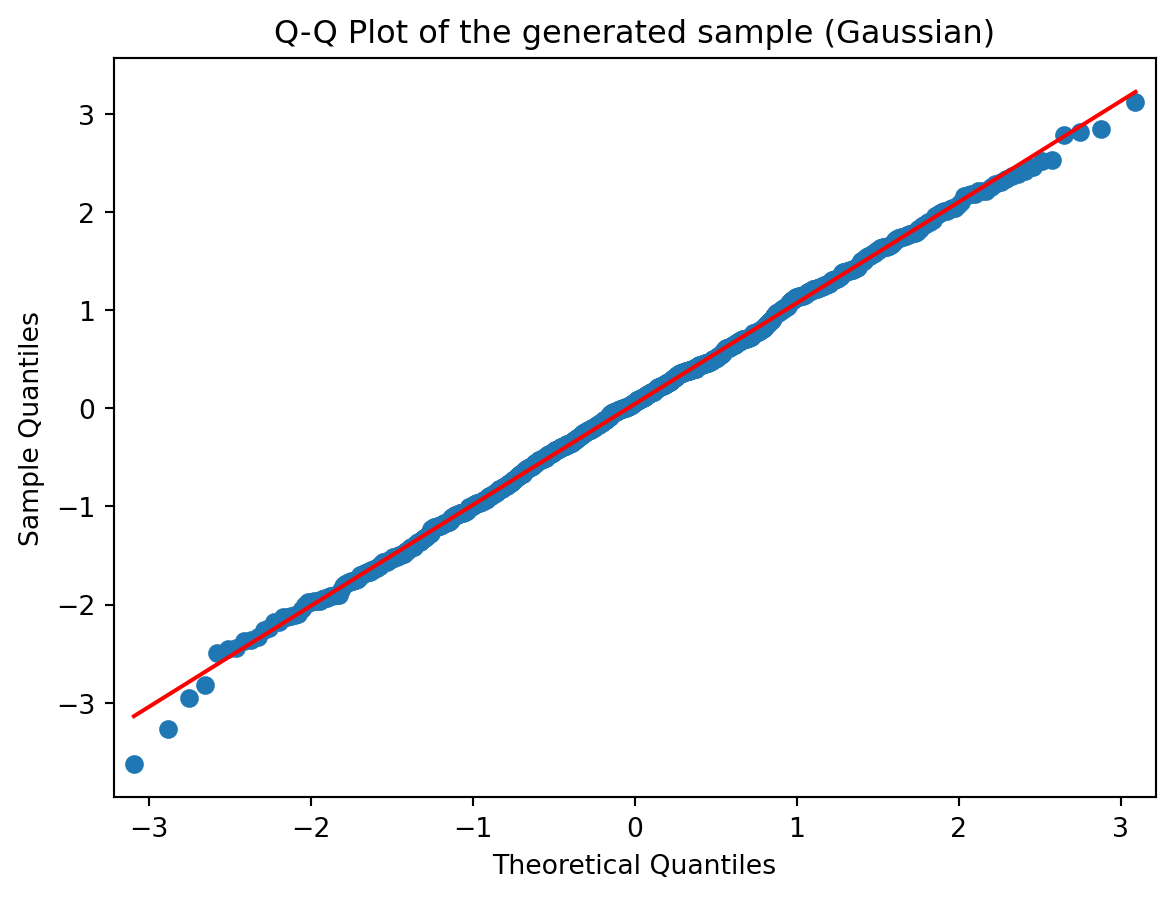
sm.qqplot(sample_norm, line='r')
plt.title('Q-Q Plot of the generated sample (Gaussian)')
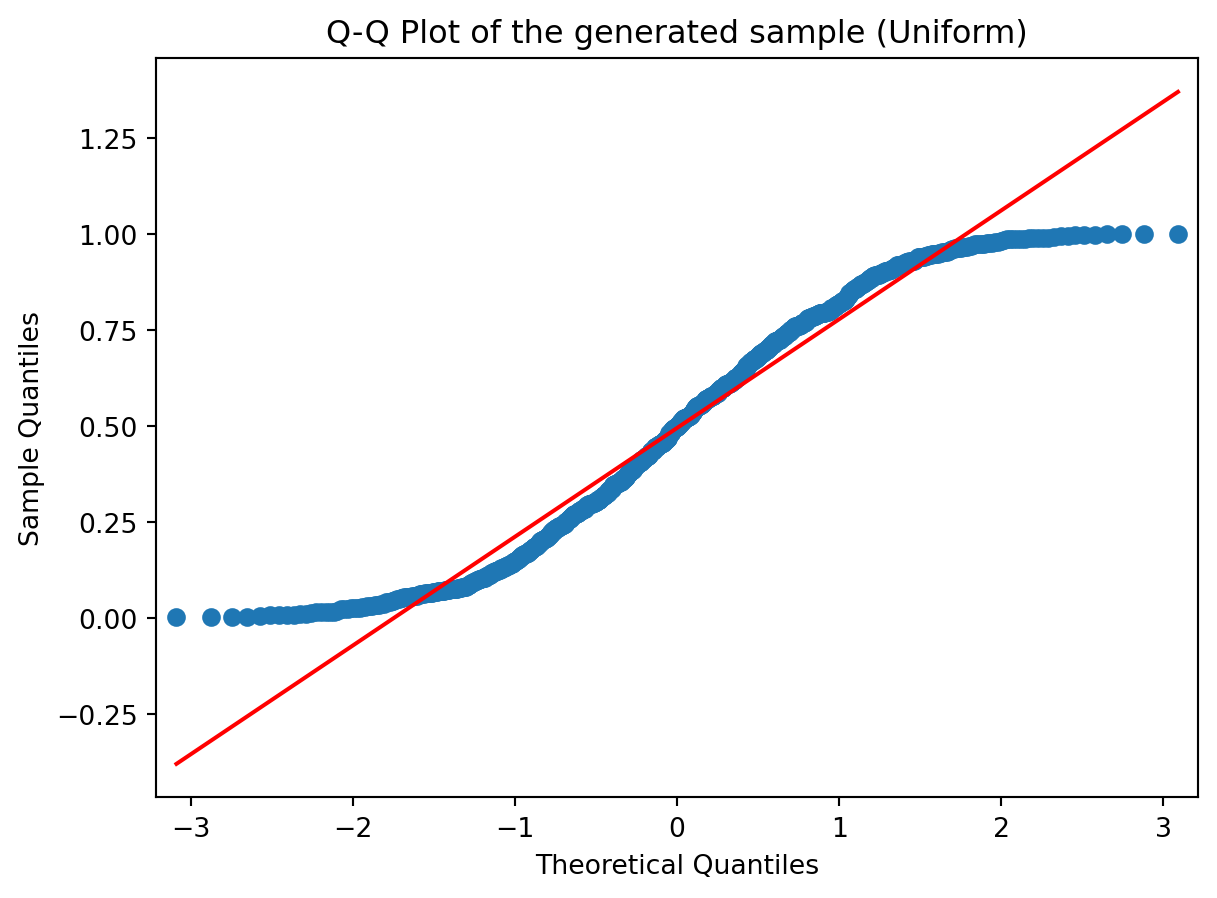
sm.qqplot(sample_unif, line='r')
plt.title('Q-Q Plot of the generated sample (Uniform)');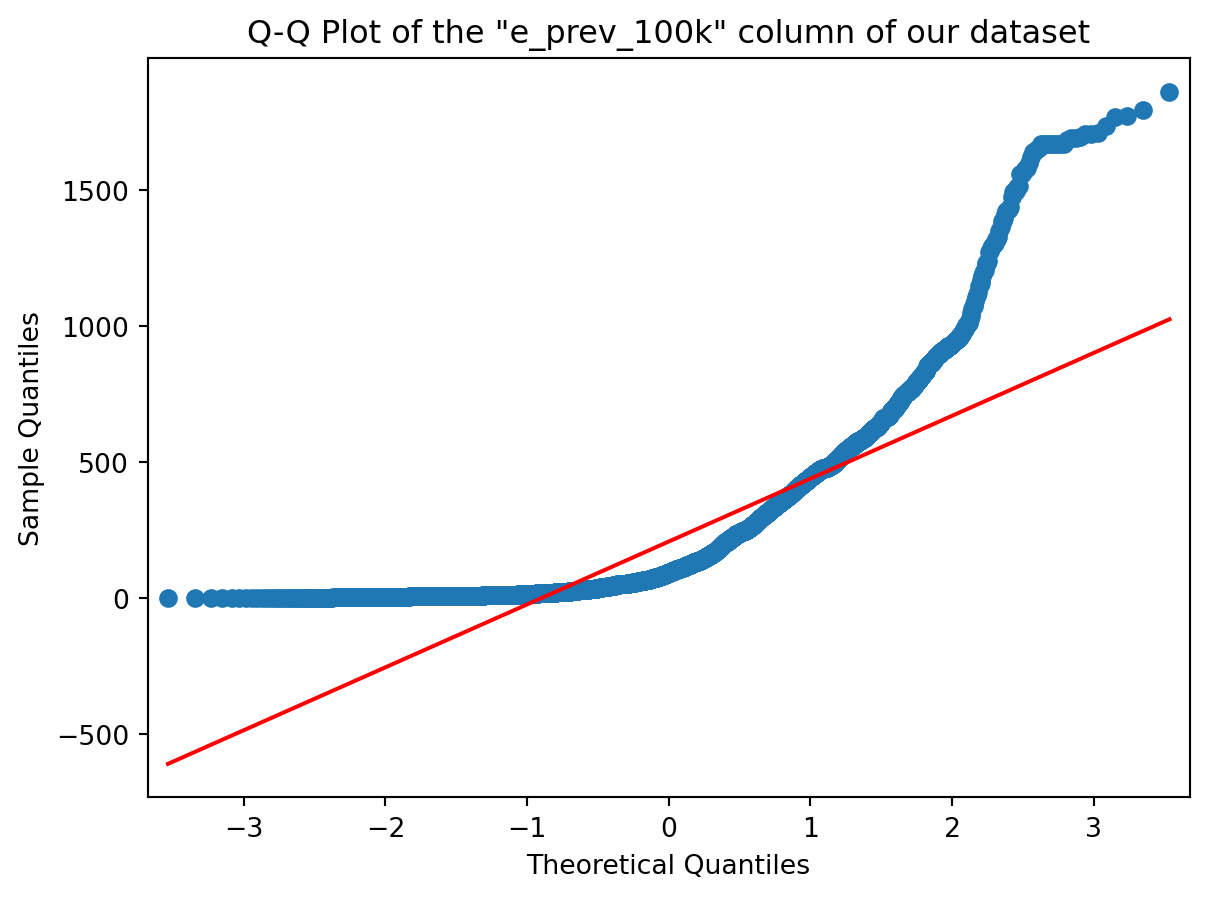

Question: Have a look at the slides from Week 03 for different shapes of data distributions.

Done? Now try to guess the shape of the distribution of our selected column (shape of its histogram) from its Q-Q Plot above.

Go ahead and change the colname variable (bullet point 1 above) into a different column name (that you can pick from the list you have just before bullet point 1 (but do pick a numeric column). And re-execute the code from bullet points 1 and 2 and you’ll see your new Q-Q plot of the column you just picked.

Visualise the column on a histogram and reflect on whether the shape you inferred from Q-Q plots and the shape of the histogram match:

# Histogramming the column we picked (not sure the verb exists though)
plt.figure(figsize=(12, 5))
plt.subplot(1,2,1)
plt.title('Histogram of "{}"'.format(colname))
plt.hist(col)
plt.subplot(1,2,2)
plt.title('Histogram of Log "{}"'.format(colname))
plt.hist(np.log(col));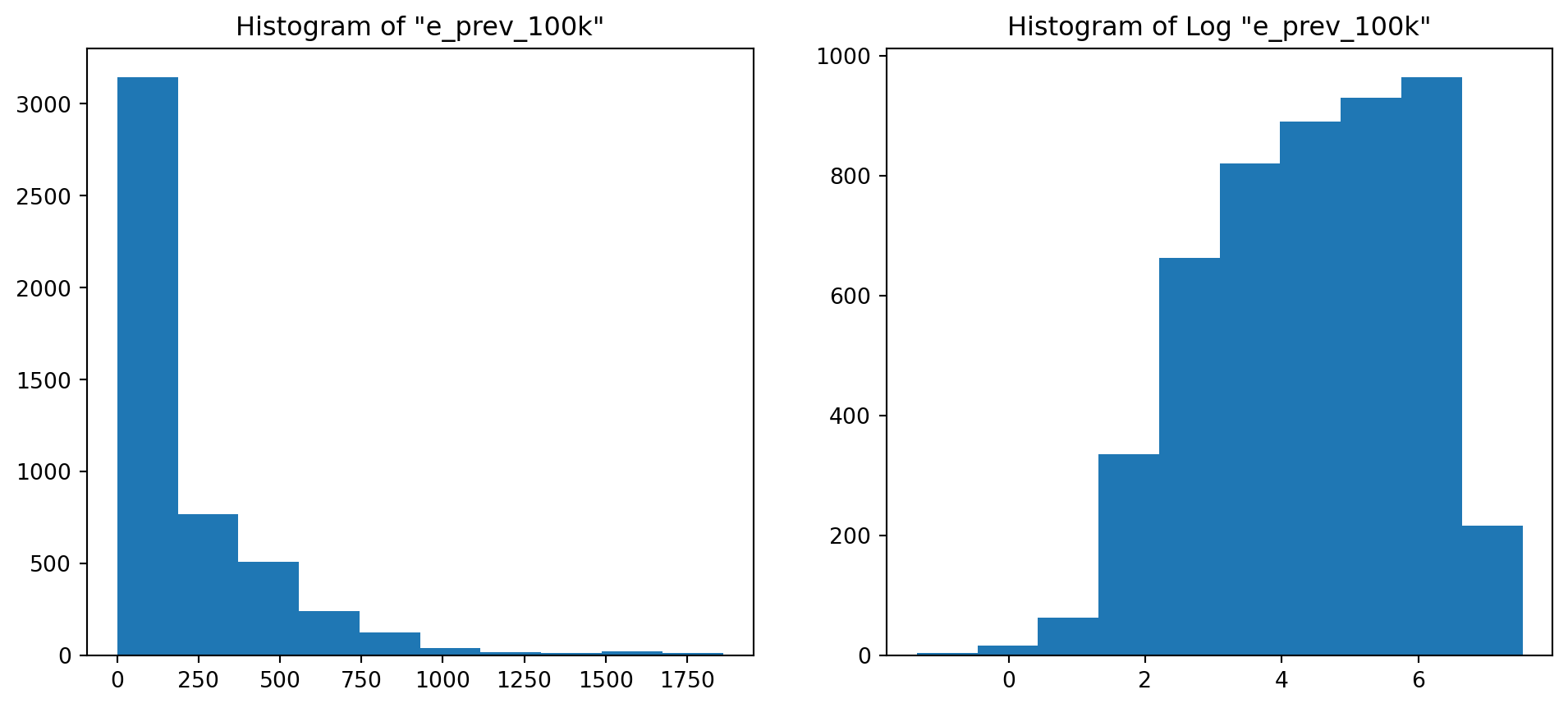

Of course it does ! From the shape of the Q-Q Plot above (convex, slope upwards) and the video slide of Q-Q Plots from Week 3 (slides 64 and 65), we could tell before looking at the histogram that our distribution was right tailed (or positively skewed if you’re into complex vocabulary, lol). And it is !

11.3 Distributions, Sampling

1.3.1) Inspecting the effect of sample size on descriptive statistics

# Defining a few variables se we can change their values easily without having to change the rest of the code
n = [5, 20, 100, 2000]
stds = [0.5, 1, 3]

# Initializing empty 2D arrays where we're going to store the results of our simulation
mean = np.empty([len(n), len(stds)])
std = np.empty([len(n), len(stds)])
skewness = np.empty([len(n), len(stds)])
kurtos = np.empty([len(n), len(stds)])

# Conducting the experiments and storing the results in the respective 2D arrays
for i, sample_size in enumerate(n):
    for j, theoritical_std in enumerate(stds):
        sample = np.random.normal(loc=0, scale=theoritical_std, size=sample_size)
        mean[i,j] = sample.mean()
        std[i,j] = sample.std()
        skewness[i,j] = skew(sample)
        kurtos[i,j] = kurtosis(sample)

# Turning the mean 2D array into a pandas dataframe
mean = pd.DataFrame(mean, columns = stds, index = n)
mean = mean.rename_axis('Sample Size').rename_axis("Standard Deviation", axis="columns")

# Turning the std 2D array into a pandas dataframe
std = pd.DataFrame(std, columns = stds, index = n)
std = std.rename_axis('Sample Size').rename_axis("Standard Deviation", axis="columns")

# Turning the skewness 2D array into a pandas dataframe
skewness = pd.DataFrame(skewness, columns = stds, index = n)
skewness = skewness.rename_axis('Sample Size').rename_axis("Standard Deviation", axis="columns")

# Turning the kurtosis 2D array into a pandas dataframe
kurtos = pd.DataFrame(kurtos, columns = stds, index = n)
kurtos = kurtos.rename_axis('Sample Size').rename_axis("Standard Deviation", axis="columns")

print("GAUSSIAN DISTRIBUTION\n")
print('Results for the Mean :')
mean # This is a dataframe containing the means of the samples generated with different values of std and sample size
print('Results for the Standard Deviation :')
std # This is a dataframe containing the standard deviations of the samples generated with different values of std and sample size
print('Results for the Skewness :')
skewness # This is a dataframe containing the skews of the samples generated with different values of std and sample size
print('Results for the Kurtosis :')
kurtos # This is a dataframe containing the kurtosis of the samples generated with different values of std and sample size

GAUSSIAN DISTRIBUTION

Results for the Mean :
Results for the Standard Deviation :
Results for the Skewness :
Results for the Kurtosis :

Standard Deviation	0.5	1.0	3.0
Sample Size
5	-1.319596	-0.541286	-0.943096
20	-0.979621	-0.895258	-0.507967
100	0.500608	-0.273542	-0.167292
2000	-0.011085	0.048641	-0.150579

# are the outputs overwritten? Try this instead
# concatenate the dataframes
combined_df = pd.concat([mean, std, skewness, kurtos], keys=['Mean', 'Standard Deviation', 'Skewness', 'Kurtosis'])

# Print combined DataFrame
print(combined_df)

Standard Deviation                   0.5       1.0       3.0
                   Sample Size                              
Mean               5           -0.100390 -0.216905 -1.786216
                   20          -0.005641  0.253152 -0.115252
                   100         -0.056784  0.005723 -0.789052
                   2000        -0.007882  0.011537 -0.028742
Standard Deviation 5            0.191937  0.925385  1.729559
                   20           0.488156  0.814340  3.773621
                   100          0.545432  1.047675  2.999077
                   2000         0.495096  0.995928  2.968200
Skewness           5            0.252509 -0.981395  0.006100
                   20           0.012524  0.083944  0.164795
                   100         -0.249811 -0.091323  0.254610
                   2000         0.081759 -0.087429 -0.010352
Kurtosis           5           -1.319596 -0.541286 -0.943096
                   20          -0.979621 -0.895258 -0.507967
                   100          0.500608 -0.273542 -0.167292
                   2000        -0.011085  0.048641 -0.150579

Basically, the more data you have (the bigger your sample), the more accurate your empirical estimates are going to be. Observe, for example, the values of mean (1st DataFrame) and variance (2nd DataFrame) for the 2000 sample size (last row). In the first one, the values are all close to 0, because we generated our sample from a Gaussian with mean 0, and the values in the second one are all close to the values in the column names (which refer to the variance of the distribution of the sample). This means that for with a sample size of 2000, our estimates are really close to the “True” values (with which we generated the sample). Also, the Skew of a Gaussian distribution should be 0, and it is confirmed in the 3rd DataFrame where the values are close to 0 in the last row (i.e big sample size).

2) Same as before but with a Poisson distribution (which has just one parameter lambda instead of 2 like the gaussian)

# Defining a few variables so we can change their values easily without having to change the rest of the code
n = [5, 20, 100, 2000]
lambd = [0.5, 1, 3] # In a gaussian we had two parameters, a var specified here and a mean we chose to be 0 
# everywhere. Here we have one parameter called lambda.

# Initializing empty 2D arrays where we're going to store the results of our simulation
mean = np.empty([len(n), len(lambd)])
std = np.empty([len(n), len(lambd)])
skewness = np.empty([len(n), len(lambd)])
kurtos = np.empty([len(n), len(lambd)])

# Conducting the experiments and storing the results in the respective 2D arrays
for i, sample_size in enumerate(n):
    for j, theoritical_lambd in enumerate(lambd):
        #**********************************************************************
        sample = np.random.poisson(lam = theoritical_lambd, size = sample_size) # THIS IS WHAT WE CHANGED FROM ABOVE
        #**********************************************************************
        mean[i,j] = sample.mean()
        std[i,j] = sample.std()
        skewness[i,j] = skew(sample)
        kurtos[i,j] = kurtosis(sample)

# Turning the mean 2D array into a pandas dataframe
mean = pd.DataFrame(mean, columns = lambd, index = n)
mean = mean.rename_axis('Sample Size').rename_axis("Lambda", axis="columns")

# Turning the std 2D array into a pandas dataframe
std = pd.DataFrame(std, columns = lambd, index = n)
std = std.rename_axis('Sample Size').rename_axis("Lambda", axis="columns")

# Turning the skewness 2D array into a pandas dataframe
skewness = pd.DataFrame(skewness, columns = lambd, index = n)
skewness = skewness.rename_axis('Sample Size').rename_axis("Lambda", axis="columns")

# Turning the kurtosis 2D array into a pandas dataframe
kurtos = pd.DataFrame(kurtos, columns = lambd, index = n)
kurtos = kurtos.rename_axis('Sample Size').rename_axis("Lambda", axis="columns")

print("POISSON DISTRIBUTION\n")
print('Results for the Mean :')
mean # This is a dataframe containing the means of the samples generated with different values of std and sample size
print('Results for the Standard Deviation :')
std # This is a dataframe containing the standard deviations of the samples generated with different values of std 
#and sample size
print('Results for the Skewness :')
skewness # This is a dataframe containing the skews of the samples generated with different values of std and sample 
#size
print('Results for the Kurtosis :')
kurtos # This is a dataframe containing the kurtosis of the samples generated with different values of std and sample 
#size

POISSON DISTRIBUTION

Results for the Mean :
Results for the Standard Deviation :
Results for the Skewness :
Results for the Kurtosis :

Lambda	0.5	1.0	3.0
Sample Size
5	-1.833333	-1.153061	-1.490806
20	-0.141090	-0.466761	-0.124442
100	0.209814	0.349051	0.171191
2000	1.998405	0.724436	0.578576

# Same as above: The outputs overwritten, so try this instead, and note that the mean, std, skewness, kurtos dataframes will now have been overwritten
combined_poisson_df = pd.concat([mean, std, skewness, kurtos], keys=['Mean', 'Standard Deviation', 'Skewness', 'Kurtosis'])
print(combined_poisson_df)

Lambda                               0.5       1.0       3.0
                   Sample Size                              
Mean               5            0.400000  0.800000  4.400000
                   20           0.450000  0.950000  3.200000
                   100          0.410000  1.070000  3.000000
                   2000         0.492500  1.019500  3.017500
Standard Deviation 5            0.489898  0.748331  1.854724
                   20           0.589491  0.973396  1.503330
                   100          0.584722  1.106842  1.562050
                   2000         0.712000  0.998559  1.751911
Skewness           5            0.408248  0.343622  0.157988
                   20           0.926296  0.750575  0.540393
                   100          1.103171  0.967842  0.299103
                   2000         1.451837  0.904064  0.626630
Kurtosis           5           -1.833333 -1.153061 -1.490806
                   20          -0.141090 -0.466761 -0.124442
                   100          0.209814  0.349051  0.171191
                   2000         1.998405  0.724436  0.578576

Just remember, the lambda parameter that defines the Poisson distribution is also the mean of the distribution. This is confirmed in the first DataFrame where the values (means of samples) are close to the column labels (theoretical lambda which is also equal to theoretical mean), especially in the last row.

11.4 Robust Statistics

1.4.1) Choose a number of columns with different shapes, for instance, “e_prev_100k_hi” is left skewed or some columns where the variation is high or you notice potential outliers. You can make use of a series of boxplots to exploratively analyse the data for outliers

# Listing the columns
df_tuber.columns

Index(['country', 'iso2', 'iso3', 'iso_numeric', 'g_whoregion', 'year',
       'e_pop_num', 'e_prev_100k', 'e_prev_100k_lo', 'e_prev_100k_hi',
       'e_prev_num', 'e_prev_num_lo', 'e_prev_num_hi', 'e_mort_exc_tbhiv_100k',
       'e_mort_exc_tbhiv_100k_lo', 'e_mort_exc_tbhiv_100k_hi',
       'e_mort_exc_tbhiv_num', 'e_mort_exc_tbhiv_num_lo',
       'e_mort_exc_tbhiv_num_hi', 'source_mort', 'e_inc_100k', 'e_inc_100k_lo',
       'e_inc_100k_hi', 'e_inc_num', 'e_inc_num_lo', 'e_inc_num_hi',
       'e_tbhiv_prct', 'e_tbhiv_prct_lo', 'e_tbhiv_prct_hi',
       'e_inc_tbhiv_100k', 'e_inc_tbhiv_100k_lo', 'e_inc_tbhiv_100k_hi',
       'e_inc_tbhiv_num', 'e_inc_tbhiv_num_lo', 'e_inc_tbhiv_num_hi',
       'source_tbhiv', 'c_cdr', 'c_cdr_lo', 'c_cdr_hi'],
      dtype='str')

# Alright I already know a few columns with outliers but let's try to find them together exploratively using BoxPlots
colname = 'c_cdr' # change the column name by choosing different ones from above (numeric ones)
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
plt.hist(df_tuber[colname])
plt.title('Histogram of "{}"'.format(colname))
plt.subplot(1,2,2)
plt.boxplot(df_tuber[colname]);
plt.title('Boxplot of "{}"'.format(colname));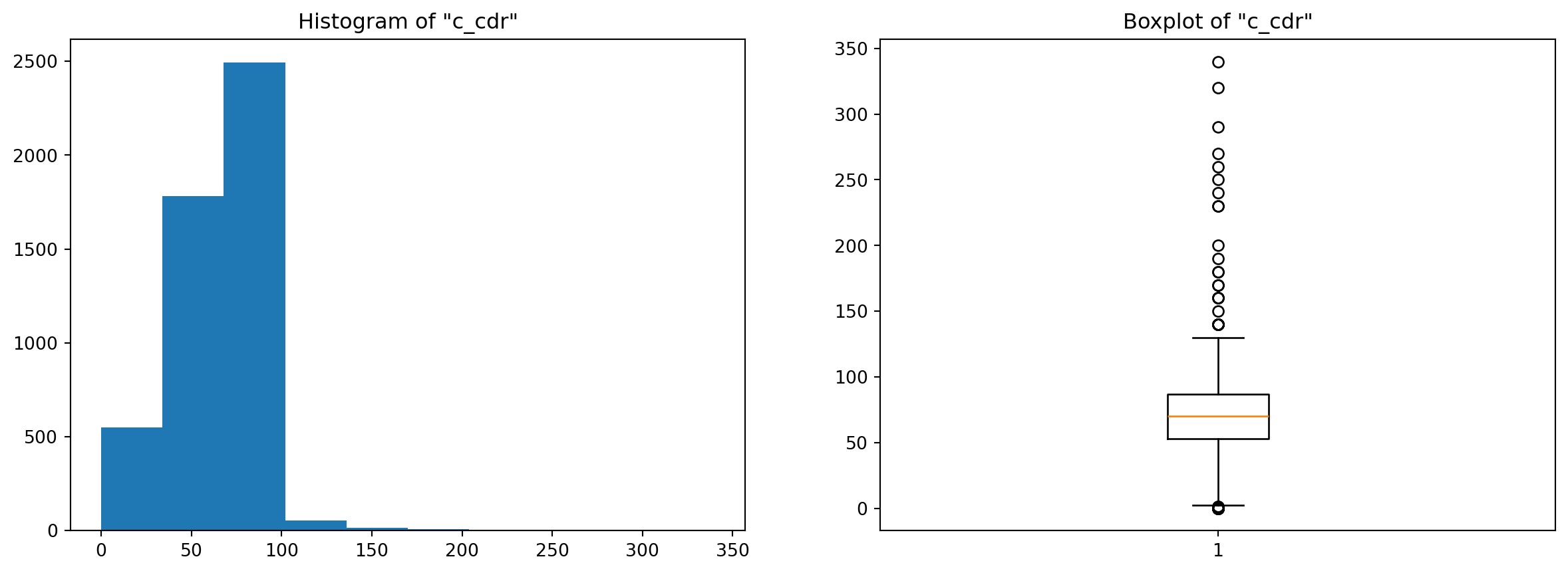

# Chosen columns : I picked 3, feel free to change them and experiment
chosen_colnames = ['e_pop_num', 'e_prev_100k', 'c_cdr']

1.4.2) For the chosen columns, estimate both the conventional and the robust descriptive statistics and compare. Observe how these pairs deviate from each other based on the characteristics of the underlying data

# Central Tendency : Mean vs Median (Median is the robust version of the mean, because it takes into account 
#the ordering of the points and not the actual values like the mean does)
df_tuber[chosen_colnames].describe().loc[['mean', '50%'], :] # The 50% is the median (50% quantile)

	e_pop_num	e_prev_100k	c_cdr
mean	2.899179e+07	207.694422	67.570706
50%	5.140332e+06	93.000000	70.000000

Look at how the values are different between the mean and the median … LOOOOOOOK ! This is why when you have a skewed (unsymmetrical) distribution it’s usually more interesting to use the median as a measure of the central tendency of the data. One important thing to note here, for the two first attributes, the mean is higher than the median, but for the last it’s the opposite. This can tell you a thing or two about the shape of your distribution : if the mean is higher than the median, this means that the distribution is skewed to the right (right tail) which pulls the mean higher. And vice-versa.

Moral of the story is … outliers can be a pain!

# Spread : Standard Deviation vs Inter-Quartile Range vs Median Absolute Deviation (MAD)
stds = df_tuber[chosen_colnames].std()
iqrs = df_tuber[chosen_colnames].quantile(0.75) - df_tuber[chosen_colnames].quantile(0.25)
medianAD = mad(df_tuber[chosen_colnames])

output = pd.DataFrame(stds, columns = ['std']).T
output = pd.concat([output, pd.DataFrame(iqrs, columns = ['IQR']).T], ignore_index=False)
output = pd.concat([output, pd.DataFrame(medianAD, columns = ['MAD'], index = chosen_colnames).T], ignore_index=False, names = ['std', 'iqr', 'mad'])
output

	e_pop_num	e_prev_100k	c_cdr
std	1.177827e+08	269.418159	25.234773
IQR	1.677193e+07	280.500000	34.000000
MAD	7.454908e+06	120.090780	25.204238

The values here are different as well, maybe more so for the “e_pop_num” attribute than the others, but that is just because of the scaling : “e_pop_num” takes big values overall compared to the other columns, which you can check with the mean values right above.

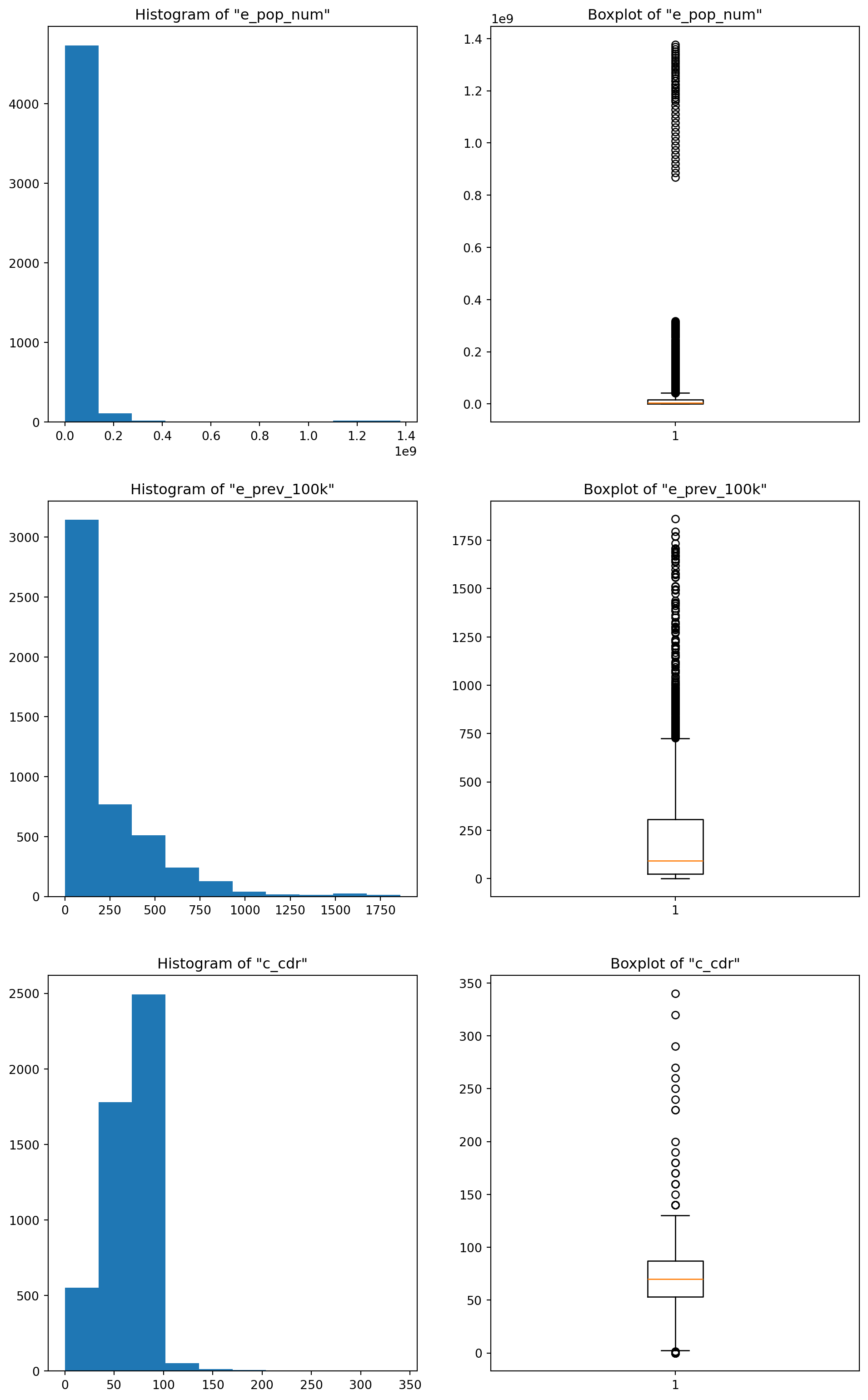
For the first attribute, the standard deviation is higher, and both the IQR and MAD are close to each other. For the second attribute, the inter-quartile range is slightly higher than the standard deviation, but the MAD is far below (less than half) the other two values, and the reason for that is a little bit involved : Basically, the standard deviation measures the spread by computing the squared deviation from the mean while the median absolute deviation evaluates the spread by computing the absolute deviation. This means that when the outliers have much bigger values than the “normal” points, the squared difference explodes (figuratively of course ;p) compared to the absolute difference. And this is actually the case for our second distribution (e_prev_100k) where most values are between 50 and 300 while many outliers lay above the 750 mark and go all the way up to 1800 (look at the boxplots below). For the third attribute the values are somewhat close, especially the std and the MAD, that’s because if you inspect the boxplot, this column doesn’t have many outliers to begin with.

Nonetheless, the differences are real, and if we don’t want to have to handle outliers, then we should be using robust statistics like the median to describe the central tendency and inter-quartile range or median absolute deviation to measure the spread of our data.

# Boxplots of the different columns
plt.figure(figsize=(12,20))

plt.subplot(3,2,1)
plt.hist(df_tuber[chosen_colnames[0]])
plt.title('Histogram of "{}"'.format(chosen_colnames[0]))
plt.subplot(3,2,2)
plt.boxplot(df_tuber[chosen_colnames[0]])
plt.title('Boxplot of "{}"'.format(chosen_colnames[0]))

plt.subplot(3,2,3)
plt.hist(df_tuber[chosen_colnames[1]])
plt.title('Histogram of "{}"'.format(chosen_colnames[1]))
plt.subplot(3,2,4)
plt.boxplot(df_tuber[chosen_colnames[1]])
plt.title('Boxplot of "{}"'.format(chosen_colnames[1]))

plt.subplot(3,2,5)
plt.hist(df_tuber[chosen_colnames[2]])
plt.title('Histogram of "{}"'.format(chosen_colnames[2]))
plt.subplot(3,2,6)
plt.boxplot(df_tuber[chosen_colnames[2]])
plt.title('Boxplot of "{}"'.format(chosen_colnames[2]));